Vesojen maksimipituus kvantiiliregression avulla
Siipilehto J., Sauvula-Seppälä T., Lehtonen M., Nykänen M., Hynynen J. (2022). Vesojen maksimipituus kvantiiliregression avulla. Metsätieteen aikakauskirja vuosikerta 2022 artikkeli 10704. https://doi.org/10.14214/ma.10704
-
Siipilehto,
Luonnonvarakeskus (Luke), Luonnonvarat, Helsinki
Sähköposti
jouni.siipilehto@luke.fi

- Sauvula-Seppälä, Luonnonvarakeskus (Luke), Tilastopalvelut, Helsinki Sähköposti tiina.sauvula-seppala@luke.fi
- Lehtonen, Luonnonvarakeskus (Luke), Luonnonvarat, Helsinki Sähköposti mika.lehtonen@luke.fi
- Nykänen, Fingrid Oyj, Helsinki Sähköposti mikko.nykanen@fingrid.fi
- Hynynen, Luonnonvarakeskus (Luke), Luonnonvarat, Helsinki Sähköposti jari.hynynen@luke.fi
Vastaanotettu 25.1.2022 Hyväksytty 3.2.2022 Julkaistu 4.2.2022
Katselukerrat 9032
Saatavilla https://doi.org/10.14214/ma.10704 | Lataa PDF

Johtoaukean raivaustyön ajoittaminen mallinnuksen motiivina
Vesakon nopea pituuskehitys on ongelma niin taimikonhoidon kuin teidenvarsien ja sähkölinjojen johtoaukeiden raivauksen näkökulmasta. Vesasyntyisten puiden pituuskasvu on siemensyntyisiä selvästi nopeampaa alkuvaiheessa, mutta siementaimen pituuskasvu saavuttaa vesan pituuskasvun muutamassa vuodessa. Siemensyntyiset lehtipuut saavuttavat vesasyntyisen taimen pituuden vasta noin 15–20 vuoden iässä. Voimalinjojen johtoaukeilla raivaus täytyy tehdä selvästi tätä aikaisemmin, joten valtavesojen pituuskehitys määrää raivausten välisen ajan pituuden. Koska johtoaukean raivaustyötä on paljon, niin vuodenaikaiseen kaatoajankohtaan ei voi juuri vaikuttaa. Kaatoajankohdan on kuitenkin huomattu vaikuttavan vesomisalttiuteen siten, että kasvukauden aikana kaadettaessa vesojen kehitys jää muita ajankohtia heikommaksi.
Vesasyntyiset koivut vesovat paremmin kuin siemensyntyiset koivut, koska niihin kehittyy runsaasti vesomiskykyisiä leposilmuja. Jos hieskoivu (Betula pubescens Ehrh.) katkotaan vuosittain tai kahden vuoden välein, sen vesomiskyky romahtaa. Toisaalta neljän vuoden välein katkaistuna vesovien kantojen määrän on havaittu pienenevän, mutta vesojen tuotoksessa ei havaittu heikkenemistä. Tärkein johtoaukean raivauksen kieroaikaan vaikuttava tekijä on, että jätettävät puut eivät suunnitellun raivauskierron kuluessa saa kasvaa määrättyä vähimmäisetäisyyttä lähemmäs johtimia. Nykyinen raivauskierto on tyypillisesti viisi vuotta Etelä-Suomessa ja noin kahdeksan vuotta Pohjois-Suomessa, ja Pohjois-Lapissa vielä tätäkin pidempi. Turvalliseen vähimmäisetäisyyteen vaikuttaa johdon jännitetaso. Kantaverkon johtojen jännitetasot vaihtelevat välillä 110–400 kV.
Luonnonvarakeskuksessa mallitettiin eri lehtipuiden vesojen maksimaalista pituuskehitystä. Mallien avulla laadittiin taulukoita eri puulajien iän mukaisesta maksimaalisesta pituuskehityksestä maan eri osiin ja erilaisille kasvupaikolle. Lisäksi laadittiin ohjelma, jolla valtavesojen pituuskehitystä voitiin ennustaa paikallisesti. Malleihin liitettiin mahdollisuus mittaushavaintoihin perustuvaan kalibrointiin. Taulukot ja ohjelma laadittiin Fingrid oyj:n käyttöön ja niitä hyödynnetään kantaverkon voimajohtojen johtoaukean raivauksen riskienhallinnassa. Kantaverkon voimajohtoja on Suomessa noin 14 000 km ja johtoaukeaa metsämaalla noin 33 500 ha. Tämä kirjoitus esittelee toteutetun mallinnuksen menetelmällisiä valintoja, erityisesti kvantiiliregressiota, sekä mallinnustulosten hyödynnettävyyttä käytännön toiminnassa.
Aineistot ja menetelmät valtavesojen pituuskehitykselle
Mallin laadinta-aineistona käytettiin Luonnonvarakeskuksen kokeita, joissa vesojen kehitystä oli seurattu. Mallinnuksen kannalta tarvittavat vesakon tunnukset olivat vesapuulaji, vesaryhmän valtavesan pituus ja vesojen ikä. Mallitusaineistoon yhdistettiin useita kokeita, kuten varsinaisia vesatutkimuksia ja taimikonhoitokokeita. Vanhimmat kokeista oli perustettu 1980-luvulla ja niistä oli saatavana pitkiä aikasarjoja, pisimmillään 38 vuotta. Yksittäiset kokeet saattoivat olla maantieteellisesti suppeita. Yhdistämällä eri kokeita saatiin aineistoa kattavammin eri puulajeista ja eri kasvupaikoilta, ja samalla aineiston maantieteellinen vaihtelu kattoi kokeita Kolarista Espooseen. Vertailujakson 1971–2000 lämpösumman vaihtelualueena se merkitsi 782–1331 °C vrk.
Kaikkia mallitettuja vesapuulajeja tavattiin sekä kangas- että turvemailta (Taulukko 1). Hieskoivulla kasvupaikkatyyppien vaihtelu oli laajinta lehtomaisesta kankaasta (OMT, kasvupaikka 2) kuivaan kankaaseen (CT, kasvupaikka 5). Joillakin puulajeilla kasvupaikkavaihtelu jäi suppeaksi – pienimmillään pihlajalla (Sorbus aucuparia L.) ja pajuilla (Salix spp. L.) vain lehtomaiseen kankaaseen (tai vastaavaan ruohoturvekankaaseen). Ylivoimaisesti suurin osa aineistosta koostui hieskoivusta, joka on yleensä valtalajina nuorissa taimikoissa. Myös rauduskoivua (Betula pendula Roth) oli runsaasti. Pajun suuri määrä johtuu turvepeltojen lyhytkiertoviljelykokeista.
| Taulukko 1. Mallitus- ja testiaineiston havaintojen määrä, kasvupaikan vaihtelu, vesojen keski- ja maksimi-ikä sekä keski- ja maksimipituus puulajien mukaan. | |||||||
| Puulaji | Havaintoja | Kasvupaikka | Lämpösumma | Ikä | Maksimi | Pituus | Maksimi |
| Raudus | 7341 | 2–4 | 1221 | 3,6 | 29 | 1,5 | 22,7 |
| Hies | 29 214 | 2–5 | 1091 | 4,7 | 38 | 1,8 | 22,0 |
| Haapa | 1170 | 2–4 | 1284 | 3,1 | 37 | 1,2 | 17,8 |
| Leppä | 847 | 2–3 | 1127 | 10,4 | 37 | 3,0 | 12,7 |
| Pihlaja | 1444 | 2 | 1305 | 2,3 | 29 | 0,7 | 7,4 |
| Pajut | 7871 | 2 | 1061 | 4,0 | 21 | 1,6 | 13,0 |
| Raita | 492 | 2–3 | 1240 | 7,5 | 37 | 1,7 | 12,4 |
| Testiaineisto | |||||||
| Raudus | 128 | 2–5 | 1176 | 4,5 | 8 | 3,3 | 5,8 |
| Hies | 117 | 2–5 | 1062 | 5,5 | 8 | 3,4 | 5,6 |
| Haapa | 55 | 2–5 | 1186 | 4,4 | 7 | 2,3 | 6,5 |
| Leppä | 72 | 2–5 | 1177 | 4,5 | 8 | 3,7 | 6,5 |
| Pihlaja | 41 | 2–5 | 1162 | 4,5 | 5 | 2,4 | 3,5 |
| Pajut | 54 | 2–4 | 1142 | 4,5 | 8 | 3,6 | 5,5 |
| Raita | 15 | 3–4 | 1069 | 5,5 | 8 | 2,2 | 4,8 |
Vuoden 2018 syksyllä mitattiin voimajohtojen seuraavan vuoden raivauskohteilta pisimpiä vesoja puulajeittain. Koealat mitattiin voimajohdon pylväiden välimaastosta siten, että arvioitiin silmämääräisesti pisin vesa ja se keskipisteenä mitattiin myös 5 m:n säteeltä muiden puulajien pisimmät vesat, jos ne olivat vähintään puolet pisimmän vesan pituudesta. Aineistoa kerättiin Uudeltamaalta, Keski-Suomesta ja Lapista Fingridin voimalinjoilta. Testiaineistoa kertyi sekä kangas- että turvemailta (Taulukko 1). Turvemaat olivat valtaosaltaan korpia. Kasvupaikkatyyppien vaihtelu oli laaja lehtomaisesta kankaasta kuivaan kankaaseen. Keski-Suomesta puuttuivat kuivan kankaan ja Lapista lehtomaisen kankaan kasvupaikan havainnot. Pajuilla kasvupaikan vaihtelu oli muita suppeampi siten, että heikoin kasvupaikka pajuilla oli kuivahko kangas. Raidasta (Salix caprea L.) oli vähän havaintoja, mutta niiden perusteella sen pituuskehitys oli testiaineistossa muita pajulajeja hitaampaa (Taulukko 1). Koska mitattu testiaineisto edusti yhtä kehitysvaihetta eli valtavesojen pituutta vuosi ennen raivausta, sen avulla voitiin testata laadittuja malleja kriittisimmässä vaiheessa. Toisaalta ikävaihtelun supistuessa eri puulajien pituuskehityksen dynamiikasta mittausajankohtaan ei testiaineiston perusteella saatu tietoa.
Koska mallitusaineisto oli hyvin heterogeeninen, siitä laadittiin kaikki puulajit sisältävä yleismalli. Yleismallin avulla saatiin kuvattua pituuskehityksen vasteet kasvupaikkaluokkaan ja lämpösummaan mahdollisimman realistisesti. Puulajeittain suurin osa aineistosta oli liian suppea näitä tunnuksia ajatellen. Malleissa oli selittävänä tekijänä ikä, josta haettiin askeltavan regression ja visuaalisen tarkastelun avulla sopivia muunnoksia. Iän (T) muunnoksia olivat ln(T), 1/(T + k), jossa k oli vakio 5 tai 10 sekä √T. Ikää ja ikämuunnosten variaatioita tarvittiin, koska puulajeilla oli erilainen iänmukainen pituuskehitys. Iän lisäksi tarvittiin kasvupaikan ja sijainnin kuvaus. Kasvupaikka kuvattiin kasvupaikkaluokille tehtyjen osoitinmuuttujien avulla. Osoitinmuuttuja saa arvon 1, kun kasvupaikka on tosi, muutoin se saa arvon 0. Osoitinmuuttujilla kuvattiin keskimääräistä heikompia viljavuustasoja: tuore (MT), kuivahko (VT) ja kuiva kangas (CT) tai vastaava turvemaan viljavuusluokka. Lisäksi turvemaat erotettiin kangasmaista osoitinmuuttujan avulla. Myös puulajit kuvattiin osoitinmuuttujilla jäännösvirheen pienentämiseksi.
Sijainti kuvattiin lämpösumman avulla, koska sijainnilla ja erityisesti lämpösummalla on havaittu selvä vaikutus pituuskehitykseen. Mallinnuksessa käytettiin lämpösumman kuntakeskiarvoja, jotka perustuvat vertailukauteen vuosilta 1971–2000. Jotta lämpösumma voitiin kätevästi liittää eri puulajien malleihin, tuli sen vaikutuksen olla keskimäärin nolla, jolloin sillä ei ollut vaikutusta mallin vakiotermiin. Tämä saatiin aikaan jakamalla lämpösumma (LS) aineiston keskimääräisellä lämpösummalla, 1100 vuorokausiastetta (°C vrk) ja ottamalla siitä logaritmi. Siten muuttuja oli muotoa ln(LS/1100). Logaritmisen lämpösumman arvo on positiivinen, kun LS > 1100 °C vrk ja negatiivinen, kun LS < 1100 °C vrk. Yleinen malli vesan pituudelle (h) voitiin kirjoittaa muotoon:
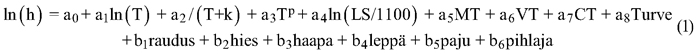
Kvantiiliregressio
Tyypillisesti regressiomallit laaditaan kuvaaman puiden keskimääräistä kehitystä pienimmän neliösumman menetelmällä. Nyt mallinnuksen kohteena oli vesojen iän mukainen maksimipituus. Mallit laadittiin SAS-ohjelmiston kvantiiliregressiolla. Kvantiilin (Q) arvolla kerrotaan, mikä vastemuuttujan ehdollinen prosenttiosuus mallilla kuvataan. Äärimmäisten järjestystunnuslukujen teorian mukaan otoskokoa kasvatettaessa uusi entistä pienempi tai suurempi arvo löytyy, vaikka todennäköisyys onkin pieni. Siksi absoluuttista maksimia on mahdoton määrittää. Käytännön maksimipituuden kuvaamiseksi valittiin 98 %:n osuus pituuden kertymäjakaumasta (Q98). Tätä suuremmalla arvolla ei estimoiduille parametreille saatu luottamusväliä kaikille puulajeille. Pituuden (h98) kehitys eri puulajeille ennustettiin logaritmiselle vesapituudelle ln(h98).
Vesojen pituuskehitys mallin ja testiaineiston mukaan
Mallin mukaan valtavesojen nopeimmat pituuden alkukehitykset olivat pajulla, hieskoivulla ja lepällä (Alnus spp. Mill.) (Kuva 1). Noin 5 vuoden jälkeen rauduskoivuvesan maksimipituus ylitti hieskoivuvesan maksimipituuden kangasmaalla. Haavan (Populus tremula L.) juurivesojen alkukehitys oli suhteellisen hidasta, mutta pituuskasvu kiihtyi vanhemmiten. Pihlajan maksimipituuden kehitys oli huomattavasti hitaampaa kuin muilla lehtipuilla (Kuva 1).
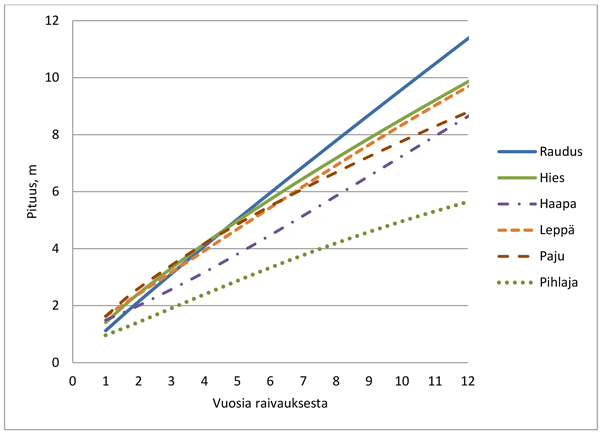
Kuva 1. Valtavesojen maksimaalinen pituuskehitys puulajeittain Etelä-Suomessa.
Puulajien väliset pituuserot olivat yleisesti yhteensopivia mallin mukaisen maksimipituuden ja testiaineiston valtavesojen keski- ja maksimipituuden välillä (Kuva 2). Malleilla suurimmat maksimipituudet vuosi ennen suunniteltua raivausta olivat hyvin tasaisesti noin neljä metriä: pajun ja hieskoivun maksimipituus 4,1 m, rauduskoivun 3,95 m ja lepän 3,97 m. Testiaineistossa lepän valtavesojen pituus (3,6 m) oli hieman pajua ja hieskoivua (3,4 m) suurempi ja rauduskoivun pituus oli keskimäärin 3,2 m. Koko testiaineistossa valtavesojen keskipituus oli oletuksen mukaisesti ennustettua maksimia pienempi (Kuva 2A). Valtavesojen maksimipituus nousi noin 5 metriin, kun havainnoiksi poimittiin koealan keskipisteestä mitatut pisimmät vesat (Kuva 2B). Samalla pajun maksimipituus ohitti hieskoivun ja lepän maksimipituuden testiaineistossa. Suurin mittaushavainto oli hieman ennustetta suurempi hieskoivulla, pihlajalla ja pajulla, ja ennuste oli puolestaan mitattua suurempi rauduskoivulla ja raidalla (Kuva 2B).
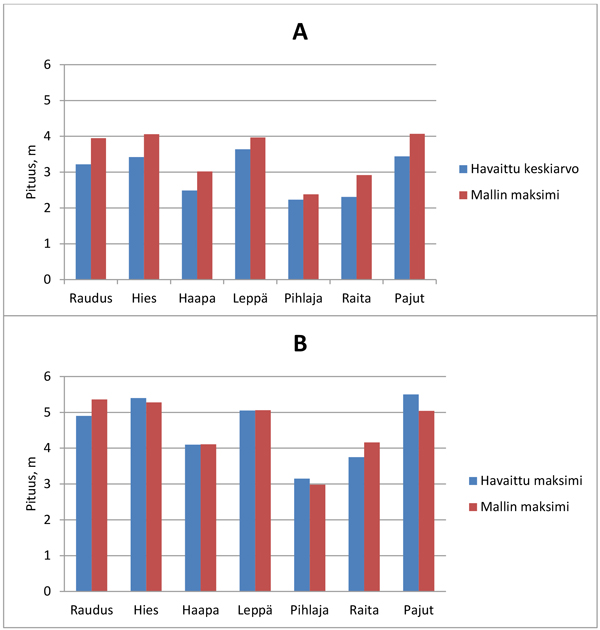
Kuva 2. Vesojen ennustettu maksimipituus (h98) ja valtavesojen keskimääräinen pituus koko testiaineistossa (A). Vastaavat suurimmat arvot testiaineiston mittauksen (koealan keskipisteen pisin vesa) ja mallin mukaan (B).
Lopuksi
Mallien mukainen lehtipuuvesojen maksimipituus vaikutti testiaineiston perusteella varsin luotettavalta. Koska malli edustaa suuresta aineistosta estimoitua maksimaalista pituuskehitystä, tulee sen arvojen ylittää testiaineiston keskimääräiset pituushavainnot. Tämä johtuu testiaineiston otannasta, jossa voimajohtojen pylväiden väliltä löydetyn pisimmän vesan (maksimin) ympäriltä mitattiin muiden puulajien pisin vesa, jos sen pituus oli vähintään puolet pisimmän vesan pituudesta. Mallien mukaan vesojen pituuden nopeimmat alkukehitykset olivat pajulla, hieskoivulla, lepällä ja rauduskoivulla. Leppä varsinaisena pioneeripuulajina on hyvin nopeakasvuinen nuorena vesana, mutta sen kasvun on havaittu taittuvan noin 15–20 vuoden iässä. Hieskoivua pidetään yleisesti rauduskoivua parempana vesojana ja se on aluksi myös nopeampi pituuskehityksessään. Mallien mukainen haavan ja pihlajan pituuskehitys viittaisi siihen, että hirven laidunnus on pitänyt sitä matalana useamman vuoden ajan.
Johtoaukeiden raivauksen kiertoaika tulee valita siten, että puut eivät ehdi kasvamaan vähimmäisetäisyyttä lähemmäs johtimia. Tätä riskiä silmällä pitäen vesojen pituuskehitystä ei voitu mallittaa perinteisellä pienimmän neliösumman menetelmällä keskipituuden kehityksenä. Sen sijaan kvantiiliregressiolla voitiin laatia malli vesojen maksimipituuden iän mukaisesta kehityksestä. Malli vastaa johtoaukeiden raivaustyön ajoittamistehtävästä kummunneeseen tarpeeseen ja on operatiivisessa käytössä sähkönsiirron riskien hallinnassa laajalla alueella.
Lähteitä
Björkdahl G (1983) Höjdutveckling hos stubbskott av vårt- och glasbjörk samt tall och gran efter mekanisk röjning. Stencil nr 18, Sveriges lantbruksuniversitet, Institutionen för skogsproduktion, Garpenberg.
Ferm A (1990) Coppicing, aboveground woody biomass and nutrition aspects of birch with specific reference to Betula pubescens. Finnish Forest Research Institute Research Papers 348. http://urn.fi/URN:ISBN:951-40-1089-2.
Hytönen J, Issakainen J (1994) Effect of repeated harvesting on biomass production and sprouting of Betula pubescens. Biomass Bioenerg 32: 944–951. https://doi.org/10.1016/S0961-9534(00)00083-0.
Hytönen J, Saarsalmi A (2015) Biomass production of coppicing grey alder and the effect of fertilization. Silva Fenn 49, article id 1260. https://doi.org/10.14214/sf.1260.
Johansson T (2008) Sprouting ability and biomass production of downy and silver birch stumps of different diameters. Biomass Bioenerg 32: 944–951. https://doi.org/10.1016/j.biombioe.2008.01.009.
Rydberg D (2000) Initial sprouting, growth and mortality of European aspen and birch after selective coppicing in central Sweden. Forest Ecol Manag 130: 27–35. https://doi.org/10.1016/S0378-1127(99)00187-5.